☞ This page belongs to resource collections on Logic and Inquiry.
A minimal negation operator  is a logical connective that says “just one false” of its logical arguments.
is a logical connective that says “just one false” of its logical arguments.
If the list of arguments is empty, as expressed in the form  then it cannot be true that exactly one of the arguments is false, so
then it cannot be true that exactly one of the arguments is false, so 
If  is the only argument, then
is the only argument, then  says that
says that  is false, so
is false, so  expresses the logical negation of the proposition
expresses the logical negation of the proposition  Wrtten in several different notations,
Wrtten in several different notations, 
If  and
and  are the only two arguments, then
are the only two arguments, then  says that exactly one of
says that exactly one of  is false, so
is false, so  says the same thing as
says the same thing as  Expressing
Expressing  in terms of ands
in terms of ands  ors
ors  and nots
and nots  gives the following form.
gives the following form.

|
As usual, one drops the dots  in contexts where they are understood, giving the following form.
in contexts where they are understood, giving the following form.

|
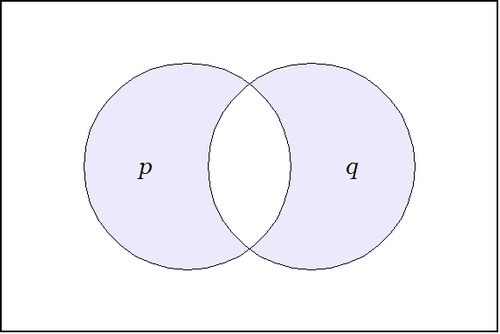
The venn diagram for  is shown in Figure 1.
is shown in Figure 1.
|

|
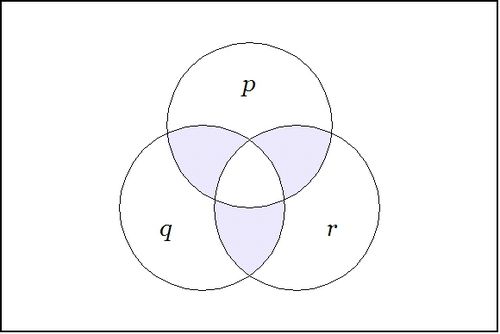
The venn diagram for  is shown in Figure 2.
is shown in Figure 2.
|

|
The center cell is the region where all three arguments  hold true, so
hold true, so  holds true in just the three neighboring cells. In other words,
holds true in just the three neighboring cells. In other words, 
Initial definition
The minimal negation operator  is a multigrade operator
is a multigrade operator  where each
where each  is a
is a  -ary boolean function defined in such a way that
-ary boolean function defined in such a way that  in just those cases where exactly one of the arguments
in just those cases where exactly one of the arguments  is
is 
In contexts where the initial letter  is understood, the minimal negation operators can be indicated by argument lists in parentheses. In the following text a distinctive typeface will be used for logical expressions based on minimal negation operators, for example,
is understood, the minimal negation operators can be indicated by argument lists in parentheses. In the following text a distinctive typeface will be used for logical expressions based on minimal negation operators, for example,  =
= 
The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation.
|
![{\displaystyle {\begin{matrix}{\texttt {()}}&=&\nu _{0}&=&0&=&\mathrm {false} \\[6pt]{\texttt {(x)}}&=&\nu _{1}(x)&=&{\tilde {x}}&=&x^{\prime }\\[6pt]{\texttt {(x,y)}}&=&\nu _{2}(x,y)&=&{\tilde {x}}y\lor x{\tilde {y}}&=&x^{\prime }y\lor xy^{\prime }\\[6pt]{\texttt {(x,y,z)}}&=&\nu _{3}(x,y,z)&=&{\tilde {x}}yz\lor x{\tilde {y}}z\lor xy{\tilde {z}}&=&x^{\prime }yz\lor xy^{\prime }z\lor xyz^{\prime }\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33172db7c4fc2a56312bfc0dadcf56ebefe3429e)
|
Formal definition
To express the general case of  in terms of familiar operations, it helps to introduce an intermediary concept:
in terms of familiar operations, it helps to introduce an intermediary concept:
Definition. Let the function  be defined for each integer
be defined for each integer  in the interval
in the interval ![{\displaystyle [1,k]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a4b2ad7a7a2603795780169e7def86702af62d) by the following equation:
by the following equation:

|
Then  is defined by the following equation:
is defined by the following equation:

|
If we think of the point  as indicated by the boolean product
as indicated by the boolean product  or the logical conjunction
or the logical conjunction  then the minimal negation
then the minimal negation  indicates the set of points in
indicates the set of points in  that differ from
that differ from  in exactly one coordinate. This makes
in exactly one coordinate. This makes  a discrete functional analogue of a point omitted neighborhood in analysis, more exactly, a point omitted distance one neighborhood. In this light, the minimal negation operator can be recognized as a differential construction, an observation that opens a very wide field. It also serves to explain a variety of other names for the same concept, for example, logical boundary operator, limen operator, least action operator, or hedge operator, to name but a few. The rationale for these names is visible in the venn diagrams of the corresponding operations on sets.
a discrete functional analogue of a point omitted neighborhood in analysis, more exactly, a point omitted distance one neighborhood. In this light, the minimal negation operator can be recognized as a differential construction, an observation that opens a very wide field. It also serves to explain a variety of other names for the same concept, for example, logical boundary operator, limen operator, least action operator, or hedge operator, to name but a few. The rationale for these names is visible in the venn diagrams of the corresponding operations on sets.
The remainder of this discussion proceeds on the algebraic boolean convention that the plus sign  and the summation symbol
and the summation symbol  both refer to addition modulo 2. Unless otherwise noted, the boolean domain
both refer to addition modulo 2. Unless otherwise noted, the boolean domain  is interpreted so that
is interpreted so that  and
and  This has the following consequences:
This has the following consequences:
| •
|
The operation  is a function equivalent to the exclusive disjunction of is a function equivalent to the exclusive disjunction of  and and  while its fiber of 1 is the relation of inequality between while its fiber of 1 is the relation of inequality between  and and 
|
| •
|
The operation  maps the bit sequence maps the bit sequence  to its parity. to its parity.
|
The following properties of the minimal negation operators  may be noted:
may be noted:
| •
|
The function  is the same as that associated with the operation is the same as that associated with the operation  and the relation and the relation 
|
| •
|
In contrast,  is not identical to is not identical to 
|
| •
|
More generally, the function  for for  is not identical to the boolean sum is not identical to the boolean sum 
|
| •
|
The inclusive disjunctions indicated for the  of more than one argument may be replaced with exclusive disjunctions without affecting the meaning, since the terms disjoined are already disjoint. of more than one argument may be replaced with exclusive disjunctions without affecting the meaning, since the terms disjoined are already disjoint.
|
Truth tables
Table 3 is a truth table for the sixteen boolean functions of type  whose fibers of 1 are either the boundaries of points in
whose fibers of 1 are either the boundaries of points in  or the complements of those boundaries.
or the complements of those boundaries.


|

|

|

|
|
|

|

|
|
|
|

|

|
|
|
|

|

|
|
|
![{\displaystyle {\begin{matrix}f_{104}\\[4pt]f_{148}\\[4pt]f_{146}\\[4pt]f_{97}\\[4pt]f_{134}\\[4pt]f_{73}\\[4pt]f_{41}\\[4pt]f_{22}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c90eb07dbf9f2525d13a44cd96e53b9e2532ac4)
|
![{\displaystyle {\begin{matrix}f_{01101000}\\[4pt]f_{10010100}\\[4pt]f_{10010010}\\[4pt]f_{01100001}\\[4pt]f_{10000110}\\[4pt]f_{01001001}\\[4pt]f_{00101001}\\[4pt]f_{00010110}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/092f35475274d501b226540d60c567c8465363c1)
|
![{\displaystyle {\begin{matrix}0~1~1~0~1~0~0~0\\[4pt]1~0~0~1~0~1~0~0\\[4pt]1~0~0~1~0~0~1~0\\[4pt]0~1~1~0~0~0~0~1\\[4pt]1~0~0~0~0~1~1~0\\[4pt]0~1~0~0~1~0~0~1\\[4pt]0~0~1~0~1~0~0~1\\[4pt]0~0~0~1~0~1~1~0\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd105d6907101356d491342a876e77fd2dd7568)
|
![{\displaystyle {\begin{matrix}{\texttt {(~p~,~q~,~r~)}}\\[4pt]{\texttt {(~p~,~q~,(r))}}\\[4pt]{\texttt {(~p~,(q),~r~)}}\\[4pt]{\texttt {(~p~,(q),(r))}}\\[4pt]{\texttt {((p),~q~,~r~)}}\\[4pt]{\texttt {((p),~q~,(r))}}\\[4pt]{\texttt {((p),(q),~r~)}}\\[4pt]{\texttt {((p),(q),(r))}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0c053c6d1f8c2f18e5c9ab5f35560a36c00947)
|
|
![{\displaystyle {\begin{matrix}f_{233}\\[4pt]f_{214}\\[4pt]f_{182}\\[4pt]f_{121}\\[4pt]f_{158}\\[4pt]f_{109}\\[4pt]f_{107}\\[4pt]f_{151}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d46e35bfb3b33bbdf528d8cdfb0c9c154074635f)
|
![{\displaystyle {\begin{matrix}f_{11101001}\\[4pt]f_{11010110}\\[4pt]f_{10110110}\\[4pt]f_{01111001}\\[4pt]f_{10011110}\\[4pt]f_{01101101}\\[4pt]f_{01101011}\\[4pt]f_{10010111}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d65e1afbead8d1cfeda439527469bd61ca5430d0)
|
![{\displaystyle {\begin{matrix}1~1~1~0~1~0~0~1\\[4pt]1~1~0~1~0~1~1~0\\[4pt]1~0~1~1~0~1~1~0\\[4pt]0~1~1~1~1~0~0~1\\[4pt]1~0~0~1~1~1~1~0\\[4pt]0~1~1~0~1~1~0~1\\[4pt]0~1~1~0~1~0~1~1\\[4pt]1~0~0~1~0~1~1~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/010d442f4851a198bca8b4369a8364280d36974d)
|
![{\displaystyle {\begin{matrix}{\texttt {(((p),(q),(r)))}}\\[4pt]{\texttt {(((p),(q),~r~))}}\\[4pt]{\texttt {(((p),~q~,(r)))}}\\[4pt]{\texttt {(((p),~q~,~r~))}}\\[4pt]{\texttt {((~p~,(q),(r)))}}\\[4pt]{\texttt {((~p~,(q),~r~))}}\\[4pt]{\texttt {((~p~,~q~,(r)))}}\\[4pt]{\texttt {((~p~,~q~,~r~))}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3ff941715fffd412e9f67854476d8028bcd11bf)
|
Charts and graphs
This Section focuses on visual representations of minimal negation operators. A few bits of terminology are useful in describing the pictures, but the formal details are tedious reading, and may be familiar to many readers, so the full definitions of the terms marked in italics are relegated to a Glossary at the end of the article.
Two ways of visualizing the space  of
of  points are the hypercube picture and the venn diagram picture. The hypercube picture associates each point of
points are the hypercube picture and the venn diagram picture. The hypercube picture associates each point of  with a unique point of the
with a unique point of the  -dimensional hypercube. The venn diagram picture associates each point of
-dimensional hypercube. The venn diagram picture associates each point of  with a unique "cell" of the venn diagram on
with a unique "cell" of the venn diagram on  "circles".
"circles".
In addition, each point of  is the unique point in the fiber of truth
is the unique point in the fiber of truth ![{\displaystyle [|s|]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc644e59e5e0c08a649b9c3b5604028802a3ca2a) of a singular proposition
of a singular proposition  and thus it is the unique point where a singular conjunction of
and thus it is the unique point where a singular conjunction of  literals is
literals is 
For example, consider two cases at opposite vertices of the cube:
| •
|
The point  with all 1's as coordinates is the point where the conjunction of all posited variables evaluates to with all 1's as coordinates is the point where the conjunction of all posited variables evaluates to  namely, the point where: namely, the point where:
|
|
|

|
| •
|
The point  with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to  namely, the point where: namely, the point where:
|
|
|

|
To pass from these limiting examples to the general case, observe that a singular proposition  can be given canonical expression as a conjunction of literals,
can be given canonical expression as a conjunction of literals,  . Then the proposition
. Then the proposition  is
is  on the points adjacent to the point where
on the points adjacent to the point where  is
is  and 0 everywhere else on the cube.
and 0 everywhere else on the cube.
For example, consider the case where  Then the minimal negation operation
Then the minimal negation operation  — written more simply as
— written more simply as  — has the following venn diagram:
— has the following venn diagram:
|


|
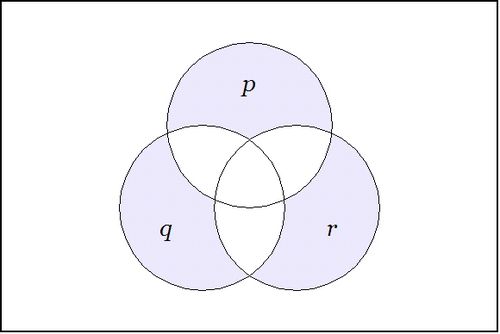
For a contrasting example, the boolean function expressed by the form  has the following venn diagram:
has the following venn diagram:
|

|
Glossary of basic terms
- Boolean domain
- A boolean domain
 is a generic 2-element set, for example,
is a generic 2-element set, for example,  whose elements are interpreted as logical values, usually but not invariably with
whose elements are interpreted as logical values, usually but not invariably with  and
and 
- Boolean variable
- A boolean variable
 is a variable that takes its value from a boolean domain, as
is a variable that takes its value from a boolean domain, as 
- Proposition
- In situations where boolean values are interpreted as logical values, a boolean-valued function
 or a boolean function
or a boolean function  is frequently called a proposition.
is frequently called a proposition.
- Basis element, Coordinate projection
- Given a sequence of
 boolean variables,
boolean variables,  each variable
each variable  may be treated either as a basis element of the space
may be treated either as a basis element of the space  or as a coordinate projection
or as a coordinate projection 
- Basic proposition
- This means that the set of objects
 is a set of boolean functions
is a set of boolean functions  subject to logical interpretation as a set of basic propositions that collectively generate the complete set of
subject to logical interpretation as a set of basic propositions that collectively generate the complete set of  propositions over
propositions over 
- Literal
- A literal is one of the
 propositions
propositions  in other words, either a posited basic proposition
in other words, either a posited basic proposition  or a negated basic proposition
or a negated basic proposition  for some
for some 
- Fiber
- In mathematics generally, the fiber of a point
 under a function
under a function  is defined as the inverse image
is defined as the inverse image 
- In the case of a boolean function
 there are just two fibers:
there are just two fibers:
- The fiber of
 under
under  defined as
defined as  is the set of points where the value of
is the set of points where the value of  is
is 
- The fiber of
 under
under  defined as
defined as  is the set of points where the value of
is the set of points where the value of  is
is 
- Fiber of truth
- When
 is interpreted as the logical value
is interpreted as the logical value  then
then  is called the fiber of truth in the proposition
is called the fiber of truth in the proposition  Frequent mention of this fiber makes it useful to have a shorter way of referring to it. This leads to the definition of the notation
Frequent mention of this fiber makes it useful to have a shorter way of referring to it. This leads to the definition of the notation ![{\displaystyle [|f|]=f^{-1}(1)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d887f350403bb5c79de68aff5a0e834a7aaadee) for the fiber of truth in the proposition
for the fiber of truth in the proposition 
- Singular boolean function
- A singular boolean function
 is a boolean function whose fiber of
is a boolean function whose fiber of  is a single point of
is a single point of 
- Singular proposition
- In the interpretation where
 equals
equals  a singular boolean function is called a singular proposition.
a singular boolean function is called a singular proposition.
- Singular boolean functions and singular propositions serve as functional or logical representatives of the points in

- Singular conjunction
- A singular conjunction in
 is a conjunction of
is a conjunction of  literals that includes just one conjunct of the pair
literals that includes just one conjunct of the pair  for each
for each 
- A singular proposition
 can be expressed as a singular conjunction:
can be expressed as a singular conjunction:
 , ,
|
|
![{\displaystyle {\begin{array}{llll}{\text{where}}&e_{j}&=&x_{j}\\[6pt]{\text{or}}&e_{j}&=&\nu (x_{j}),\\[6pt]{\text{for}}&j&=&1~{\text{to}}~k.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb46eb2e6b0bc7b5201b68f996f7949542765f52)
|
Resources
Syllabus
Focal nodes
Peer nodes
Logical operators
Related topics
Relational concepts
Information, Inquiry
Related articles
Document history
Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

































![{\displaystyle {\begin{matrix}{\texttt {()}}&=&\nu _{0}&=&0&=&\mathrm {false} \\[6pt]{\texttt {(x)}}&=&\nu _{1}(x)&=&{\tilde {x}}&=&x^{\prime }\\[6pt]{\texttt {(x,y)}}&=&\nu _{2}(x,y)&=&{\tilde {x}}y\lor x{\tilde {y}}&=&x^{\prime }y\lor xy^{\prime }\\[6pt]{\texttt {(x,y,z)}}&=&\nu _{3}(x,y,z)&=&{\tilde {x}}yz\lor x{\tilde {y}}z\lor xy{\tilde {z}}&=&x^{\prime }yz\lor xy^{\prime }z\lor xyz^{\prime }\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33172db7c4fc2a56312bfc0dadcf56ebefe3429e)


![{\displaystyle [1,k]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a4b2ad7a7a2603795780169e7def86702af62d)






































![{\displaystyle {\begin{matrix}f_{104}\\[4pt]f_{148}\\[4pt]f_{146}\\[4pt]f_{97}\\[4pt]f_{134}\\[4pt]f_{73}\\[4pt]f_{41}\\[4pt]f_{22}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c90eb07dbf9f2525d13a44cd96e53b9e2532ac4)
![{\displaystyle {\begin{matrix}f_{01101000}\\[4pt]f_{10010100}\\[4pt]f_{10010010}\\[4pt]f_{01100001}\\[4pt]f_{10000110}\\[4pt]f_{01001001}\\[4pt]f_{00101001}\\[4pt]f_{00010110}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/092f35475274d501b226540d60c567c8465363c1)
![{\displaystyle {\begin{matrix}0~1~1~0~1~0~0~0\\[4pt]1~0~0~1~0~1~0~0\\[4pt]1~0~0~1~0~0~1~0\\[4pt]0~1~1~0~0~0~0~1\\[4pt]1~0~0~0~0~1~1~0\\[4pt]0~1~0~0~1~0~0~1\\[4pt]0~0~1~0~1~0~0~1\\[4pt]0~0~0~1~0~1~1~0\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd105d6907101356d491342a876e77fd2dd7568)
![{\displaystyle {\begin{matrix}{\texttt {(~p~,~q~,~r~)}}\\[4pt]{\texttt {(~p~,~q~,(r))}}\\[4pt]{\texttt {(~p~,(q),~r~)}}\\[4pt]{\texttt {(~p~,(q),(r))}}\\[4pt]{\texttt {((p),~q~,~r~)}}\\[4pt]{\texttt {((p),~q~,(r))}}\\[4pt]{\texttt {((p),(q),~r~)}}\\[4pt]{\texttt {((p),(q),(r))}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0c053c6d1f8c2f18e5c9ab5f35560a36c00947)
![{\displaystyle {\begin{matrix}f_{233}\\[4pt]f_{214}\\[4pt]f_{182}\\[4pt]f_{121}\\[4pt]f_{158}\\[4pt]f_{109}\\[4pt]f_{107}\\[4pt]f_{151}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d46e35bfb3b33bbdf528d8cdfb0c9c154074635f)
![{\displaystyle {\begin{matrix}f_{11101001}\\[4pt]f_{11010110}\\[4pt]f_{10110110}\\[4pt]f_{01111001}\\[4pt]f_{10011110}\\[4pt]f_{01101101}\\[4pt]f_{01101011}\\[4pt]f_{10010111}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d65e1afbead8d1cfeda439527469bd61ca5430d0)
![{\displaystyle {\begin{matrix}1~1~1~0~1~0~0~1\\[4pt]1~1~0~1~0~1~1~0\\[4pt]1~0~1~1~0~1~1~0\\[4pt]0~1~1~1~1~0~0~1\\[4pt]1~0~0~1~1~1~1~0\\[4pt]0~1~1~0~1~1~0~1\\[4pt]0~1~1~0~1~0~1~1\\[4pt]1~0~0~1~0~1~1~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/010d442f4851a198bca8b4369a8364280d36974d)
![{\displaystyle {\begin{matrix}{\texttt {(((p),(q),(r)))}}\\[4pt]{\texttt {(((p),(q),~r~))}}\\[4pt]{\texttt {(((p),~q~,(r)))}}\\[4pt]{\texttt {(((p),~q~,~r~))}}\\[4pt]{\texttt {((~p~,(q),(r)))}}\\[4pt]{\texttt {((~p~,(q),~r~))}}\\[4pt]{\texttt {((~p~,~q~,(r)))}}\\[4pt]{\texttt {((~p~,~q~,~r~))}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3ff941715fffd412e9f67854476d8028bcd11bf)

![{\displaystyle [|s|]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc644e59e5e0c08a649b9c3b5604028802a3ca2a)














































![{\displaystyle [|f|]=f^{-1}(1)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d887f350403bb5c79de68aff5a0e834a7aaadee)



![{\displaystyle {\begin{array}{llll}{\text{where}}&e_{j}&=&x_{j}\\[6pt]{\text{or}}&e_{j}&=&\nu (x_{j}),\\[6pt]{\text{for}}&j&=&1~{\text{to}}~k.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb46eb2e6b0bc7b5201b68f996f7949542765f52)