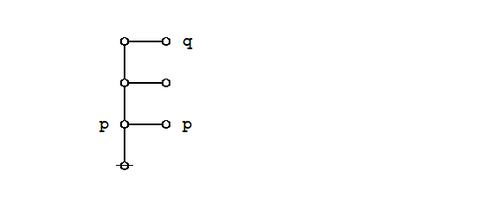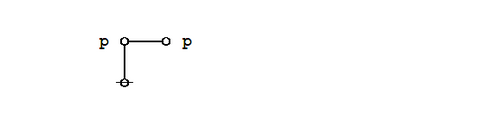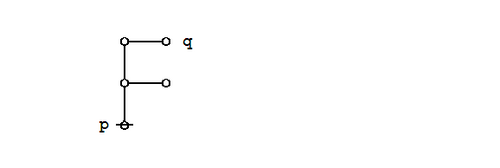Peirce's law: Difference between revisions
Jon Awbrey (talk | contribs) (plural wiki links) |
Jon Awbrey (talk | contribs) (update) |
||
| Line 169: | Line 169: | ||
===Focal nodes=== | ===Focal nodes=== | ||
* [[Inquiry Live]] | * [[Inquiry Live]] | ||
* [[Logic Live]] | * [[Logic Live]] | ||
===Peer nodes=== | ===Peer nodes=== | ||
* [http://intersci.ss.uci.edu/wiki/index.php/Peirce's_law Peirce's Law @ InterSciWiki] | |||
* [http://mywikibiz.com/Peirce's_law Peirce's Law @ MyWikiBiz] | * [http://mywikibiz.com/Peirce's_law Peirce's Law @ MyWikiBiz] | ||
* [http://ref.subwiki.org/wiki/Peirce's_law Peirce's Law @ Subject Wikis] | * [http://ref.subwiki.org/wiki/Peirce's_law Peirce's Law @ Subject Wikis] | ||
* [http://en.wikiversity.org/wiki/Peirce's_law Peirce's Law @ Wikiversity] | |||
* [http://beta.wikiversity.org/wiki/Peirce's_law Peirce's Law @ Wikiversity Beta] | * [http://beta.wikiversity.org/wiki/Peirce's_law Peirce's Law @ Wikiversity Beta] | ||
===Logical operators=== | ===Logical operators=== | ||
| Line 269: | Line 257: | ||
===Related articles=== | ===Related articles=== | ||
* [http:// | {{col-begin}} | ||
{{col-break}} | |||
* [http:// | * [http://intersci.ss.uci.edu/wiki/index.php/Cactus_Language Cactus Language] | ||
* [http://intersci.ss.uci.edu/wiki/index.php/Futures_Of_Logical_Graphs Futures Of Logical Graphs] | |||
* [http:// | * [http://intersci.ss.uci.edu/wiki/index.php/Propositional_Equation_Reasoning_Systems Propositional Equation Reasoning Systems] | ||
{{col-break}} | |||
* [http:// | * [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_:_Introduction Differential Logic : Introduction] | ||
* [http://intersci.ss.uci.edu/wiki/index.php/Differential_Propositional_Calculus Differential Propositional Calculus] | |||
* [http:// | * [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_and_Dynamic_Systems_2.0 Differential Logic and Dynamic Systems] | ||
{{col-break}} | |||
* [http:// | * [http://intersci.ss.uci.edu/wiki/index.php/Prospects_for_Inquiry_Driven_Systems Prospects for Inquiry Driven Systems] | ||
* [http://intersci.ss.uci.edu/wiki/index.php/Introduction_to_Inquiry_Driven_Systems Introduction to Inquiry Driven Systems] | |||
* [http:// | * [http://intersci.ss.uci.edu/wiki/index.php/Inquiry_Driven_Systems Inquiry Driven Systems : Inquiry Into Inquiry] | ||
{{col-end}} | |||
* [http:// | |||
==Document history== | ==Document history== | ||
| Line 289: | Line 276: | ||
Portions of the above article were adapted from the following sources under the [[GNU Free Documentation License]], under other applicable licenses, or by permission of the copyright holders. | Portions of the above article were adapted from the following sources under the [[GNU Free Documentation License]], under other applicable licenses, or by permission of the copyright holders. | ||
* [http://intersci.ss.uci.edu/wiki/index.php/Peirce's_law Peirce's Law], [http://intersci.ss.uci.edu/ InterSciWiki] | |||
* [http://mywikibiz.com/Peirce's_law Peirce's Law], [http://mywikibiz.com/ MyWikiBiz] | * [http://mywikibiz.com/Peirce's_law Peirce's Law], [http://mywikibiz.com/ MyWikiBiz] | ||
* [http:// | * [http://planetmath.org/PeircesLaw Peirce's Law], [http://planetmath.org/ PlanetMath] | ||
* [http:// | * [http://wikinfo.org/w/index.php/Peirce's_law Peirce's Law], [http://www.wikinfo.org/w/ Wikinfo] | ||
* [http://en.wikiversity.org/wiki/Peirce's_law Peirce's Law], [http://en.wikiversity.org/ Wikiversity] | |||
* [http:// | |||
* [http://beta.wikiversity.org/wiki/Peirce's_law Peirce's Law], [http://beta.wikiversity.org/ Wikiversity Beta] | * [http://beta.wikiversity.org/wiki/Peirce's_law Peirce's Law], [http://beta.wikiversity.org/ Wikiversity Beta] | ||
* [http://en.wikipedia.org/w/index.php?title=Peirce%27s_law&oldid=60606482 Peirce's Law], [http://en.wikipedia.org/ Wikipedia] | * [http://en.wikipedia.org/w/index.php?title=Peirce%27s_law&oldid=60606482 Peirce's Law], [http://en.wikipedia.org/ Wikipedia] | ||
[[Category:Inquiry]] | [[Category:Inquiry]] | ||
Revision as of 15:34, 7 November 2015
☞ This page belongs to resource collections on Logic and Inquiry.
Peirce's law is a formula in propositional calculus that is commonly expressed in the following form:
Peirce's law holds in classical propositional calculus, but not in intuitionistic propositional calculus. The precise axiom system that one chooses for classical propositional calculus determines whether Peirce's law is taken as an axiom or proven as a theorem.
History
Here is Peirce's own statement and proof of the law:
|
A fifth icon is required for the principle of excluded middle and other propositions connected with it. One of the simplest formulae of this kind is: This is hardly axiomatical. That it is true appears as follows. It can only be false by the final consequent being false while its antecedent is true. If this is true, either its consequent, is true, when the whole formula would be true, or its antecedent is false. But in the last case the antecedent of that is must be true. (Peirce, CP 3.384). |
Peirce goes on to point out an immediate application of the law:
|
From the formula just given, we at once get: where the is used in such a sense that means that from every proposition follows. With that understanding, the formula states the principle of excluded middle, that from the falsity of the denial of follows the truth of (Peirce, CP 3.384). |
Note. Peirce uses the sign of illation “” for implication. In one place he explains “” as a variant of the sign “” for less than or equal to; in another place he suggests that is an iconic way of representing a state of affairs where in every way that it can be, is
Graphical proof
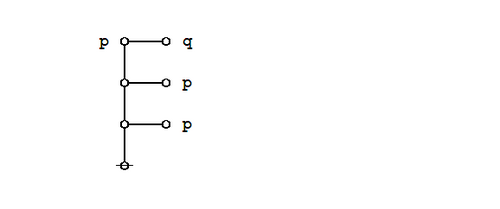
Under the existential interpretation of Peirce's logical graphs, Peirce's law is represented by means of the following formal equivalence or logical equation.
 |
(1) |
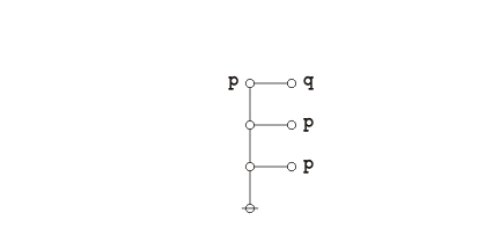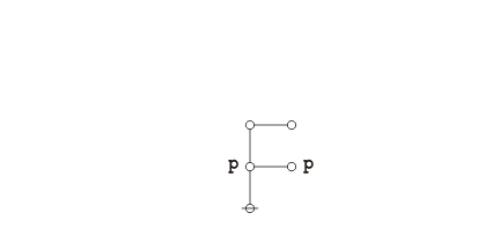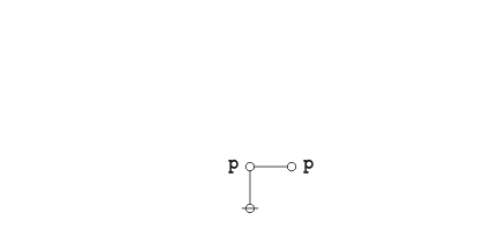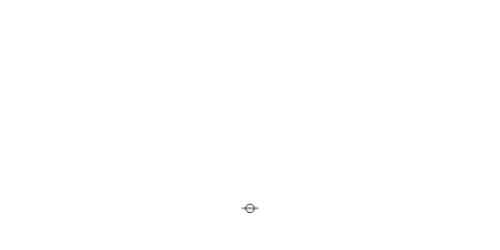
Proof. Using the axiom set given in the entry for logical graphs, Peirce's law may be proved in the following manner.
|
(2) |
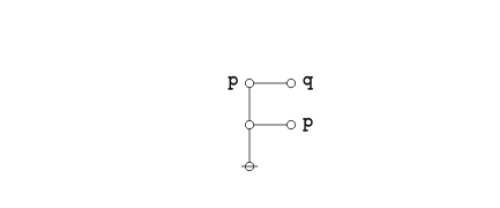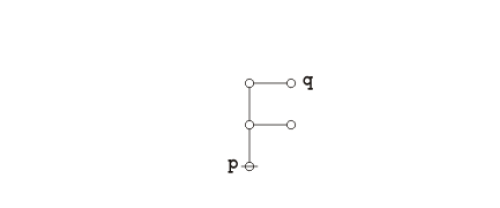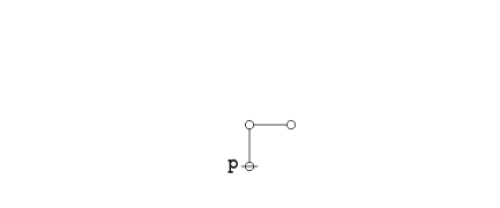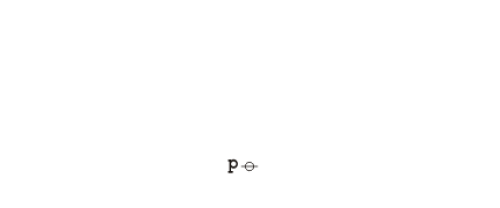
The following animation replays the steps of the proof.
|
(3) |
Equational form
A stronger form of Peirce's law also holds, in which the final implication is observed to be reversible:
Proof 1
Given what precedes, it remains to show that:
But this is immediate, since for any proposition
Proof 2
Representing propositions as logical graphs under the existential interpretation, the strong form of Peirce's law is expressed by the following equation:
 |
(4) |
Using the axioms and theorems listed in the article on logical graphs, the equational form of Peirce's law may be proved in the following manner:
|
(5) |
The following animation replays the steps of the proof.
|
(6) |
Bibliography
- Peirce, Charles Sanders (1885), "On the Algebra of Logic : A Contribution to the Philosophy of Notation", American Journal of Mathematics 7 (1885), 180–202. Reprinted (CP 3.359–403), (CE 5, 162–190).
- Peirce, Charles Sanders (1931–1935, 1958), Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA. Cited as (CP volume.paragraph).
- Peirce, Charles Sanders (1981–), Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN. Cited as (CE volume, page).
Syllabus
Focal nodes
Peer nodes
- Peirce's Law @ InterSciWiki
- Peirce's Law @ MyWikiBiz
- Peirce's Law @ Subject Wikis
- Peirce's Law @ Wikiversity
- Peirce's Law @ Wikiversity Beta
Logical operators
Related topics
Relational concepts
Information, Inquiry
Related articles
Document history
Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.
- Inquiry
- Open Educational Resource
- Peer Educational Resource
- Artificial Intelligence
- Combinatorics
- Computer Science
- Cybernetics
- Equational Reasoning
- Formal Languages
- Formal Systems
- Graph Theory
- History of Logic
- History of Mathematics
- Knowledge Representation
- Logic
- Logical Graphs
- Mathematics
- Philosophy
- Semiotics
- Visualization